
Some Interesting Things About Dice
A number cube has six sides. Each side is numbered, one through six. If we roll one cube, one is as likely to come up as six. We say the probability of getting a one, two, three, four, five or six is one out of six in every case. Each number is equally likely to come up.
The situation is very different for a pair of number cubes. If we roll a pair of dice and add them together the possible combinations are two, three, four, five, six, seven, eight, nine, ten, eleven, and twelve. A shorthand way of writing these possible outcomes is the set= {2,3,4,5,6,7,8,9,10,11,12}. If roll a pair of dice many times we would not expect a two to come up as many times as a six or an eight. Why? Take a look at the table below. It lists all the ways two cubes can be arranged.
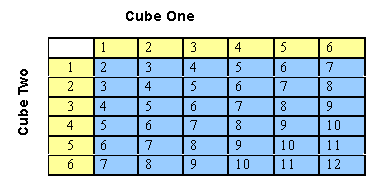
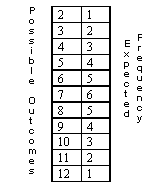
Please note that there are 6 ways to get the sum of 7 but only 1 way to get a 2. If we roll the dice many times, we would expect, on the average, to get many more sevens than twos.
All together there are 36 possible outcomes. Count them in the table above. The probability of getting a 2 is only one out of thirty-six or 1/36, but the probability of getting a 7 is six out of thirty-six or 6/36. We have six times as many chances of getting a seven than we do a two. If we throw a pair of dice a few times this pattern may not be very obvious. We need to perform this experiment many times to see the pattern. That’s where a computer program will help save us time.
Roll The Dice
If you roll a pair of number cubes there are several
possible outcomes. They are 2, 3, 4, 5, 6, 7, 8, 9,
10, 11, and 12. Is each one of these outcomes equally
likely, or will some numbers come up more than others?
We could perform this experiment with real dice, but it
would take several hundred trials and that would take
a lot of time tossing, adding, recording and summarizing.
There is an easier way. You can let the computer do the
work for you. All you have to do is tell the computer
how many times you want to toss the dice. The computer
will toss, add, and record, and summarize each event.
This will give you more time for the important job of
looking for the pattern. To get good results start with
a hundred tosses, and then gradually increase the sample
size to ten-thousand. Computers are amazingly fast.
Imagin how long it would take you to toss a pair of dice
10,000 times, and summarize your results.
Copyright 2021, William Johnson